Buscar en este blog...
Un espacio metamatemático de divulgación de la historia, aplicaciones, ejercicios interesantes, curiosidades y hechos fascinantes de la Matemática como una manera distinta acercarse a ella.
Entradas
Mostrando las entradas de 2015
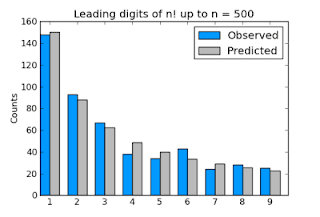
Cifras iniciales en los Factoriales
- Obtener vínculo
- Correo electrónico
- Otras apps
Epifanías
- Obtener vínculo
- Correo electrónico
- Otras apps
Discusiones en torno al Trabajo y la Energía
- Obtener vínculo
- Correo electrónico
- Otras apps